Young Researcher Paper Award 2025
🥇Winners
🥇Winners
Print: ISSN 0914-4935
Online: ISSN 2435-0869
Sensors and Materials
is an international peer-reviewed open access journal to provide a forum for researchers working in multidisciplinary fields of sensing technology.
Online: ISSN 2435-0869
Sensors and Materials
is an international peer-reviewed open access journal to provide a forum for researchers working in multidisciplinary fields of sensing technology.
Tweets by Journal_SandM
Sensors and Materials
is covered by Science Citation Index Expanded (Clarivate Analytics), Scopus (Elsevier), and other databases.
Instructions to authors
English 日本語
Instructions for manuscript preparation
English 日本語
Template
English
Publisher
MYU K.K.
Sensors and Materials
1-23-3-303 Sendagi,
Bunkyo-ku, Tokyo 113-0022, Japan
Tel: 81-3-3827-8549
Fax: 81-3-3827-8547
MYU Research, a scientific publisher, seeks a native English-speaking proofreader with a scientific background. B.Sc. or higher degree is desirable. In-office position; work hours negotiable. Call 03-3827-8549 for further information.

MYU Research
(proofreading and recording)

MYU K.K.
(translation service)

The Art of Writing Scientific Papers
(How to write scientific papers)
(Japanese Only)
is covered by Science Citation Index Expanded (Clarivate Analytics), Scopus (Elsevier), and other databases.
Instructions to authors
English 日本語
Instructions for manuscript preparation
English 日本語
Template
English
Publisher
MYU K.K.
Sensors and Materials
1-23-3-303 Sendagi,
Bunkyo-ku, Tokyo 113-0022, Japan
Tel: 81-3-3827-8549
Fax: 81-3-3827-8547
MYU Research, a scientific publisher, seeks a native English-speaking proofreader with a scientific background. B.Sc. or higher degree is desirable. In-office position; work hours negotiable. Call 03-3827-8549 for further information.

MYU Research
(proofreading and recording)

MYU K.K.
(translation service)

The Art of Writing Scientific Papers
(How to write scientific papers)
(Japanese Only)
Sensors and Materials, Volume 29, Number 6(1) (2017)
Copyright(C) MYU K.K.
Copyright(C) MYU K.K.
|
pp. 645-657
S&M1357 Research Paper of Special Issue https://doi.org/10.18494/SAM.2017.1477 Published: June 7, 2017 Finite Geometry Permutation Decoding for Wireless Sensor Network Applications [PDF] Jyun-Jie Wang and Chi-Yuan Lin (Received September 27, 2016; Accepted December 5, 2016) Keywords: Euclidean geometry code, energy efficiency, sensor network, network lifetime, majority logic decoding, permutation
In this study, we propose a novel coding method, called geometry permutation decoding (GPD), for square sensor topologies. The GPD algorithm provides a two-dimensional geometry construction and decodes information sequences based on this construction. The two-dimensional construction for square wireless sensor networks (WSNs) is suitable for employing channel coding, especially product codes and finite geometry codes, and for detecting multiple error patterns. A majority logic decoding (MLD) is a less correcting efficient but simpler-to-implement decoding method. To improve the drawback of the less correcting capacity, the GPD algorithm not only gives better bit error rates at low decoding complexity but also provides a new solution suitable for decoding in two-dimensional WSNs. In particular, this decoding work in the two-dimensional WSNs is achieved over the bit level without a packet level so that the overhead in the network layer can be reduced.
Corresponding author: Chi-Yuan Lin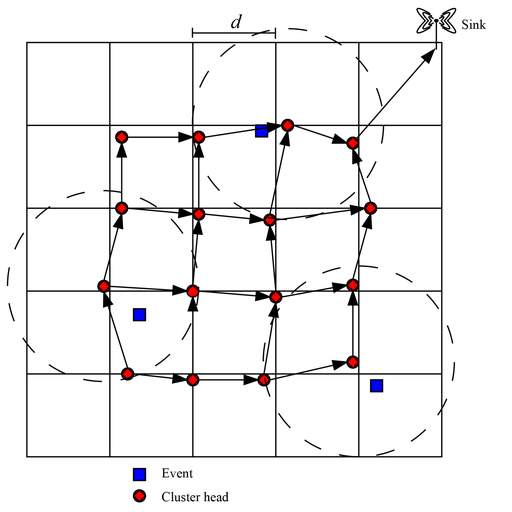 Cite this article Jyun-Jie Wang and Chi-Yuan Lin, Finite Geometry Permutation Decoding for Wireless Sensor Network Applications, Sens. Mater., Vol. 29, No. 6, 2017, p. 645-657. |
Forthcoming Regular Issues
Forthcoming Special Issues
Special Issue on Novel Sensors, Materials, and Related Technologies on Artificial Intelligence of Things Applications
Guest editor, Teen-Hang Meen (National Formosa University), Wenbing Zhao (Cleveland State University), and Cheng-Fu Yang (National University of Kaohsiung)
Call for paper
Special Issue on Unique Physical Behavior at the Nano to Atomic Scales
Guest editor, Takahiro Namazu (Kyoto University of Advanced Science)
Call for paper
Special Issue on Support Systems for Human Environment Utilizing Sensor Technology and Image Processing Including AI
Guest editor, Takashi Oyabu (Nihonkai International Exchange Center)
Call for paper
Special Issue on Mobile Computing and Ubiquitous Networking for Smart Society
Guest editor, Akira Uchiyama (The University of Osaka) and Jaehoon Paul Jeong (Sungkyunkwan University)
Call for paper
Special Issue on Advanced Materials and Technologies for Sensor and Artificial- Intelligence-of-Things Applications (Selected Papers from ICASI 2026)
Guest editor, Sheng-Joue Young (National United University)
Conference website
Call for paper
Special Issue on Innovations in Multimodal Sensing for Intelligent Devices, Systems, and Applications
Guest editor, Jiahui Yu (Research scientist, Zhejiang University), Kairu Li (Professor, Shenyang University of Technology), Yinfeng Fang (Professor, Hangzhou Dianzi University), Chin Wei Hong (Professor, Tokyo Metropolitan University), Zhiqiang Zhang (Professor, University of Leeds)
Call for paper
-
For more information of Special Issues (click here)
-
Special Issue on Signal Collection, Processing, and System Integration in Automation Applications
- Accepted papers (click here)
- High-precision Autonomous Driving Map Quality Inspection Indicator System and Evaluation Method
Chengcheng Li, Ming Dong, Hongli Li, Xunwen Yu, Yongxuan Liu, and Chong Zhang
- High-precision Autonomous Driving Map Quality Inspection Indicator System and Evaluation Method
- Accepted papers (click here)
- Scalable Real-time Energy Monitoring, Analysis, and Optimization in Five-axis Machine Tools: An Industrial Internet of Energy-based Approach
Swami Nath Maurya, Kun-Ying Li, Windu Aditya Nur Faeza, and Yue-Feng Lin
- Scalable Real-time Energy Monitoring, Analysis, and Optimization in Five-axis Machine Tools: An Industrial Internet of Energy-based Approach
Guest editor, Hsiung-Cheng Lin (National Chin-Yi University of Technology)
Call for paper
Special Issue on Advanced Materials and Technologies for Sensor and Artificial- Intelligence-of-Things Applications (Selected Papers from ICASI 2025)
Guest editor, Sheng-Joue Young (National United University)
Conference website
Call for paper
Special Issue on Multisource Sensors for Geographic Spatiotemporal Analysis and Social Sensing Technology Part 5
Guest editor, Prof. Bogang Yang (Beijing Institute of Surveying and Mapping) and Prof. Xiang Lei Liu (Beijing University of Civil Engineering and Architecture)
Special Issue on Advanced GeoAI for Smart Cities: Novel Data Modeling with Multi-source Sensor Data
Guest editor, Prof. Changfeng Jing (China University of Geosciences Beijing)
Call for paper
Special Issue on Materials, Devices, Circuits, and Analytical Methods for Various Sensors (Selected Papers from ICSEVEN 2025)
Guest editor, Chien-Jung Huang (National University of Kaohsiung), Mu-Chun Wang (Minghsin University of Science and Technology), Shih-Hung Lin (Chung Shan Medical University), Ja-Hao Chen (Feng Chia University)
Conference website
Call for paper
Special Issue on Sensing and Data Analysis Technologies for Living Environment, Health Care, Production Management, and Engineering/Science Education Applications (2025)
Guest editor, Chien-Jung Huang (National University of Kaohsiung), Rey-Chue Hwang (I-Shou University), Ja-Hao Chen (Feng Chia University), Ba-Son Nguyen (Lac Hong University)
Call for paper
Special Issue on Advances in Sensors and Computational Intelligence for Industrial Applications
Guest editor, Chih-Hsien Hsia (National Ilan University)
Call for paper
Special Issue on AI-driven Sustainable Sensor Materials, Processes, and Circular Economy Applications
Guest editor, Shih-Chen Shi (National Cheng Kung University) and Tao-Hsing Chen (National Kaohsiung University of Science and Technology)
Call for paper
- Accepted papers (click here)
Copyright(C) MYU K.K. All Rights Reserved.
